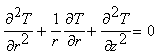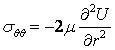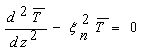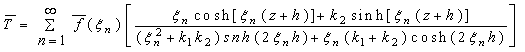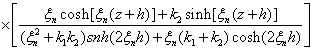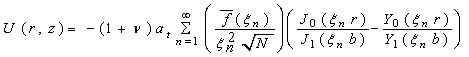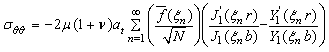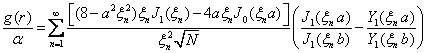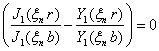• Thesis to Book with ISBN
• Aim And Scope
• Article in Press
• Editorial Board
• Current Issue
• Archives
• Publication Charges
• Authors Information
• Contact Us
• Paper Format

[Abstract] [PDF] [HTML] [Linked References]

Study of an Exact Solution of Steady-State Thermoelastic problem of an Annular Disc

Gaikwad P. B.^1* and Ghadle K. P.²

¹Department of Mathematics, Dr. Babasaheb Ambedkar Marathwada University, Aurangabad (MS) India.

²Department of Mathematics, Dr. Babasaheb Ambedkar Marathwada University, Aurangabad (MS) India.

^*Corresponding Addresses

[email protected]

Abstract: In this paper, an attempt is made to determine the unknown temperature, displacement and stress functions on outer curved surface, where as third kind boundary condition maintained on upper surface and zero temperature is maintained on lower boundary surface. The governing heat conduction has been solved by using finite Hankel transform technique. The results are obtained in series form in term of Bessel�s functions. The results for unknown displacements and stresses have been computed numerically.

Key words: Steady- state, Thermoelastic problem, Hankel transforms, Annular Disc.

Introduction:

During the second half of the twentieth century, non �isothermal problems of the theory of elasticity became increasingly important. This is due mainly to their many applications in diverse fields. First, the high velocity of modern aircrafts give rise to an aerodynamic heating, which produce intense thermal stresses reducing the strength of aircrafts structure.

Two dimensional transient problems for a thick annular disc in thermoelasticity studied by (Dange et al., 2009). An inverse temperature field of theory of thermal stresses investigated by (Grysa et al; 1981) while A note of quasi �static thermal stresses in steady state thick annular disc and an inverse quasti-static thermal stresses in thick annular disc are studied by (Gaikwad et al; 2010). An inverse problem of coupled thermal stress fields in a circular cylinder considered by (Noda; 1989).

In this paper, in the first problem, an attempt is made to determine the unknown temperature, displacement and stress functions on curved surfaces, where an arbitrary heat is applied on the upper surface (z = h) and maintained zero on lower surface (z = - h) while in second problem third kind boundary condition is maintained on lower and upper surface of an annular disc. The governing heat conduction equation has been solved by using Hankel transform technique. The results are obtained in series form in terms of Bessel�s functions and illustrated numerically.

---------------------------------------------

*2000 Mathematics Subject Classifications: primary 35A25, secondary 74M99, 74K20.

This paper contains new and novel contribution of thermal stresses in an annular disc under steady state. The above results were obtained under steady state field. The result presented here are useful in engineering problem particularly in the determination of the state of strain in an annular disc constituting foundations of containers for hard gases or liquids, in the foundations for furnaces etc.

2. Results Required:

The finite Hankel transform over the variable r and it inverse transform defined in [7].

                                                                                     (2.1)

                                                                                  (2.2)

where                                                                                         (2.3)

                                                                             (2.4)

The normality constant

                                                                                     (2.5)

and ,,���..are the roots transcendental equation,

                                                                                                  (2.6)

 is Bessel function of the first kind of the order  and Bessel function of the second kind of the order .

3. Formulation of the Problem:

 Consider an annular disc of thickness occupying space, .

The differential equation governing the displacement potential function is given in [7] as,

                                                                                             (3.1)

         with  at  and                                                     (3.2)

here

 and   are the poisson�s ratio and the linear coefficient of thermal expansion of the material of the plate and T is the temperature of the plate satisfying the differential equation  

                                                                                                (3.3) Subject to the boundary conditions

               at                                                                     (3.4)

      at                                                                           (3.5)

            at                                                                      (3.6)

The stress functions and are given by,

                                                                                                         (3.7)

                                                                                                    (3.8)

where is the Lame�s constant, while each of the stress functions and  are zero within the plate in the plane state of stress. The equations (3.1) to (3.8) constitute the mathematical formulation of the problem under consideration.

4. Solution of the Problem:

Applying finite Hankel transform defined in [6] to the equations (3.1) to Eq. (3.6), one obtain                                                                                         (4.1)

where  is the Hankel transform of T.

On solving Eq. (4.1) under the conditions given in Eq. (3.5) and Eq. (3.6).one obtains

                                                                                                                           (4.2)

On applying the inverse Hankel transform defied in Eq. (2.2) to Eq. (4.2), one obtain the expression for the temperature as

                                                       (4.3)

                                                     (4.4)

where

                                                                                   (4.5)

Equation (4.3) and (4.4) are the desired solution of the given problem.

Determination of Thermoelastic Displacements:

Substituting the values of T(r, z) from Eq. (4.3) in Eq. (3.1) one obtains the thermoelastic displacement function U(r, z) as,

                                                     (4.6)

Determination of Stresses Functions:

Using Eq. (4.6) in Eq. (3.7) and (3.8), one obtains the stress functions  and  as,

                                                      (4.7)

                                                          (4.8)

Special Case and Numerical Calculations:

Set   in (4.4) one obtains

                                                            (4.9)

The numerical calculation have been carried out for steel (SN 50 C) plate with parameters ,, ,thermal diffusivity  and poisons ratio ,while, ,,,, being the positive roots of transcendental equation    as in [6].

Concluding Remarks:

In this paper, we have discussed the steady �state thermoelastic problem for an annular disc on outer curved surface of the annular disc, whereas arbitrary heat is applied on the upper surface and zero temperature is maintained on lower surface.

The finite Hankel transform transform technique is used to obtain the numerical results. The thermoelastic behavior is examined such as unknown temperature, displacement and stresses that are obtained can be applied to the design of useful structures or in engineering applications. Also any particular case of special interest can be derived by assigning suitable values to the parameters and functions in the expressions [4.3], [4.4], [4.6]-[4.9].

References:

[1]   Dange, W.K., Khobraade, N.W., and Varghese, V., Two dimensional transient problems for a thick annular disc in thermoelasticity.  Far East Journal of Applied Mathematics, Vol.43, 205-219, 2009.

[2]   Grysa, K., Cialkowski, M. J and Kaminski H., An inverse temperature field of theory of thermal stresses. NUCL. Eng. Des. Vol.64. 161-184, 1981.

[3]   Gaikwad K.R., Ghadle K.P., A note of Quasi-Static Thermal Stresses in Steady State Thick  Annular Disc.Acta Ciencia Indica,Vol.XXXVI M,No.3,385, 2010.

[4]   Gaikwad K.R.,Ghadle K.P., An Inverse Quasi-Static Thermal Stresses in Thick Annular  Disc., International Journal of Applied Mathematics & Statistics. Vol.19. D10, 2010.

[5]   Nowacki, W., Thermoelasticity Mass. Addition-Wesley Publication Co. Chapter-1, 1962.

[6]   Ozisik N.M., Boundary value problem of Heat Conduction, International text book, Comp. Scranten, Pennsylvania, pp.481-492, 1968.

[7]   Sneddon, I.N., The use of integral transform, McGraw Hill, New York, 235-238, 1972.

[8]   Noda, N., An inverse problem of coupled thermal stress fields in a circular cylinder, JSME,Intermational Journal,Ser.A.32, pp.791-797, 1989.