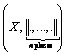Some Fixed Point Theorems for Contractive Type Mapping in n-banach spaces

Mukti Gangopadhyay^1*, Mantu Saha^2� AND A. P. Baisnab³

¹Calcutta Girls B.T. College, 6/1 Swinhoe Street, Kolkata-700019, (WB) INDIA.

²Department of Mathematics, the University of Burdwan, Burdwan-713104, (WB) INDIA.

³Lady Brabourne College, Kolkata, (WB) INDIA.

Corresponding Addresses:

^*[email protected], ^�[email protected]

Abstract: Some Fixed Point Theorems for a class of mappings with contractive iterates in a setting of n-Banach spaces have been proved.

2000 Mathematics subject classification: 47H10, 54H25.

Keywords: n-Banach space, fixed point, contraction.

1.  Introduction

The concept of 2-normed spaces was introduced and studied by German Mathematician Siegfried G�hler [11], [12], [13], [14] in a series of paper as appeared in 1960�s. Later on Misiak [1] had also developed the notion of an n-norm in 1989. The concept on n-inner product spaces is also due to Misiak who had studied the same as early as 1980 , see [1]. Following this one sees systematic development in theory of linear n-normed spaces as made by S. S. Kim and Y. J. Cho [10], R. Maleceski [7] and H. Gunawan and Mashadi [5]. H. Dutta and B. Surendra Reddy in [6], have shown that under certain cases convergence and completion in a n-normed space is equivalent to those in (n � r) norm, r = 1, 2, �, n � 1. For related works of n-metric spaces and n-inner product spaces one may see [1], [2] and [3].

Recently H. Gunawan and M. Mashadi in [5] have proved some fixed point theorems for contractive mappings acting over a finite dimensional n-Banach space. In this paper we also present some fixed point theorems for mappings with contractive iterates supposed to act on any n-Banach space.

2. We recall some preliminary Definitions related to our findings as presented here below.

Definition 2.1: Given a natural number n, let X  be a real vector space of dimension  (d may be infinity). A real valued function  on  satisfying following four properties,

(i)  if and only if  are linearly dependent in X.

(ii)  is invariant under permutation of ,

(iii)  for every

(iv)  for all y and z in X, is called an n-norm over X and the pair  is called an n-normed spaces.

Definition 2.2.: A sequence  in an n-normed space  is said to converge to an element  (in the n-norm) whenever  for every .

Definition 2.3.: A sequence  in an n-normed space  is said to be a Cauchy sequence with respect to n-norm if  for every .

Definition 2.4.: If every Cauchy sequence in X converges to an element , then X is said to be complete (with respect to the n-norm).

A complete n-normed space is called an n-Banach space.

Definition 2.5.: Let X be a n-Banach space and T be a self mapping of X. T is said to be continuous at x if for every sequence  in X,  as  implies  as  in X.

Example 2.1: Take the function space  of all square integrable functions over the closed interval [0,1]. Then  where �s are polynomials with  and  becomes a linearly independent set in . For a natural number n define an n-norm over  as  (n factors)  Reals denoted by

 and given by

, where .

Note that in an n-normed space  we have for instance  and

 for all  and for all scalars . Then it is a routine argument to see that  is an n-normed Banach space (see section 2.1 of [5]).

 

 

3. Theorem 3.1

Let T be a self-mapping of X such that there exists h where  and for all

       (3.1)

then T has a unique fixed point z in X with  for each .

Proof: Let, and define a recursive sequence  by

.

Then by (3.1) we have,

  

           

.

Now  is impossible, because . So we need examining case (i) and (ii) only as under.

Case (i) : Suppose max   

Therefore                                              (3.2)            

Case (ii) : Suppose

                       

Therefore  

   implies

                                                   (3.3)

From (3.2) and (3.3) we have

 for all k and for all .

So,  for all k and for all .

Proceeding in this way

                 , where .

If , for , we have

 as .

That means  is Cauchy sequence in X and let .

Again for ,

                       

Passing on  we have .

Therefore  and z is a fixed point of T where  for each .

Uniqueness of z is obvious.

Theorem 3.2: Let X be a n-Banach space with . Let  be a sequence of mappings such that

(i)

             for all  and ,  with .                                                                                    (3.4)

and (ii)  for each . Then T has a unique fixed point z in X such that ,  being the unique fixed point of

Proof: Taking limit as  in (3.4) we obtain

 for all  and hence T satisfies (3.4), Hence by Theorem 3.1, T has a unique fixed point say .

Now for ,

                                           (3.5)

Again

 implies

                (3.6)

By (3.5) and (3.6) we have,

                               

or,

                                                   

or, .

So, by routine calculation we get .

Theorem 3.3: Let X be a n-Banach space and  be a sequence of mappings with fixed point  such that  uniformly over  to satisfy,

                                                                                                                                                               (3.7)

 for allwhere                                                                                                                            

then  where z is the fixed point of T in X.

Proof: Fix , from uniform convergence of  on  there exists an integer k such that for all  and for all ,

 for all  where .                                               (3.8)

Now

                                          (3.9)

From (3.7) we get,

 since .

Now  is impossible because   and .

Hence above gives

           

Using (3.9) we have

           

                       

           

                         implies

           

i.e.,     

which equals to , for  using (3.8). Hence .

Theorem 3.4: Let S and T be two self mappings of X satisfying

           

                                    (3.10)

for all  where . Then S and T have a unique common fixed point  where  for each .

Proof: Let  and define  by  and .

Then by (3.10)

           

           

                       

           

                                                                                              (3.11)

Let    (3.12)

In case

Then

           

, gives

that means right hand side of (3.11) equals to , contrary to the case as assumed above.

Thus

By a similar argument we arrive at

Therefore (3.11) is not tenable.

Further  and therefore (3.11) gives

By exactly the same argument we produce