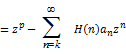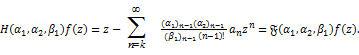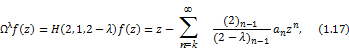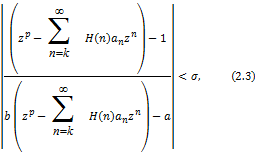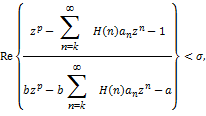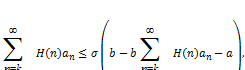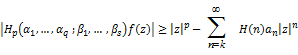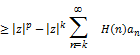|
A Subclass of 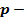 Valent and Analytic Functions Associated With Dzoik Srivastava Linear Operator Valent and Analytic Functions Associated With Dzoik Srivastava Linear Operator
Chena Ram*, Saroj Solanki#
Department of Mathematics and Statistics, Jai Narain Vyas University, Jodhpur, Rajasthan, INDIA.
Corresponding Addresses:
*[email protected], #[email protected]
1. Introduction
Let 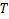 denote the class of functions of the form denote the class of functions of the form
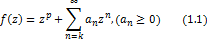
which are analytic and 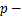 valent in the unit disk valent in the unit disk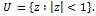
Function 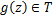 is given by is given by
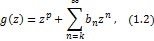
then the Hadamard product (or Convolution) of 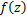 and and 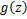 is defined by is defined by
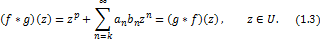
Let 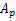 denote the subclass of denote the subclass of  consisting of functions of the form consisting of functions of the form
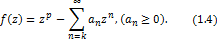 The Generalized hypergeometric function q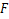 s s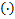 for positive real values of for positive real values of 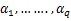 and and 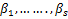 ( (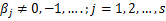 ) is defined by ) is defined by
q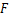 s s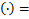 q q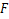 s s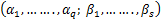 = = 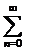 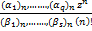 (1.5) (1.5)
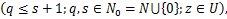
where 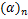 is the pochhammer symbol defined by is the pochhammer symbol defined by
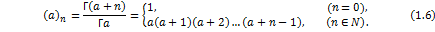
Corresponding to a function  is defined by is defined by 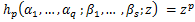 q q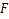 s s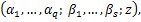 (1.7) (1.7)
The Dziok and Srivastava operator [6] 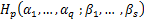 is defined by is defined by
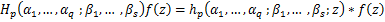
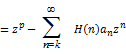 (1.8) (1.8)
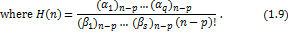
If we set 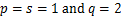 , then the linear operator , then the linear operator 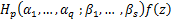 reduces to linear operator reduces to linear operator 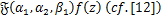 as as
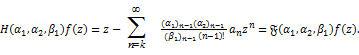 (1.10) (1.10)
If we put 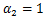 in above equation (1.10), then it reduces to Carlson-Shaffer operator [2] as in above equation (1.10), then it reduces to Carlson-Shaffer operator [2] as
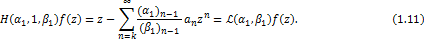
In particular, if we put 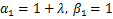 , then it reduces to Ruscheweyh operator [10] given by , then it reduces to Ruscheweyh operator [10] given by
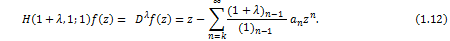
If we set 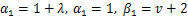 , then (1.10) reduces to Bernadi-Libera-Livingston integral operator given earlier by (see [11, 1, 8]) as , then (1.10) reduces to Bernadi-Libera-Livingston integral operator given earlier by (see [11, 1, 8]) as
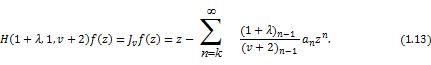 Now, we recall the following definition of fractional derivative operator due to Owa [9].
Definition1. The fractional integral of order 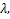 for function for function 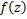 is defined by is defined by
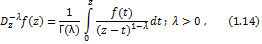
where the analytic function 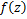 is defined in a simply-connected region of the is defined in a simply-connected region of the 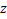 -plane containing the origin, and multiplicity of -plane containing the origin, and multiplicity of 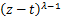 is removed by requiring is removed by requiring 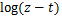 to be real when to be real when 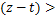 0. 0.
The fractional derivative operator of order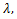 for an analytic function for an analytic function 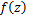 is defined by is defined by
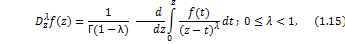
where the conditions, under which (1.15) is valid, are similar to those stated with (1.14).
Definition 2. Under the hypotheses of (1.15), the fractional derivative of function 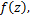 order order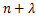 is defined by is defined by
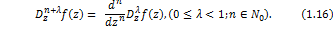
In particular case, if we let 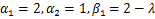 then (1.10) reduces to linear operator then (1.10) reduces to linear operator 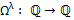 due to Srivastava and Owa [3] is defined by due to Srivastava and Owa [3] is defined by
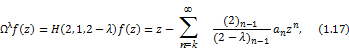
where 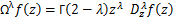 . .
For details, one can see [4, 5].
Definition 3. A function 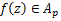 defined by (1.4) is said to be in the class defined by (1.4) is said to be in the class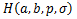 if it satisfied the following relations (cf. [7]) if it satisfied the following relations (cf. [7])
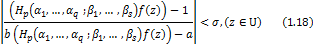
A function  defined by (1.4) is said to be in the class defined by (1.4) is said to be in the class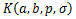 if and only if if and only if
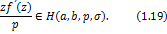
2. Coefficient Estimates
Theorem 2.1. Let the function 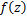 be defined by (1.4). Then be defined by (1.4). Then 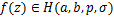 if and if and
only if
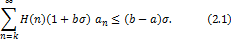
The result is sharp for the function
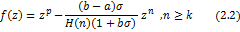
where 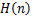 is defined by (1.9). is defined by (1.9).
Proof. Let 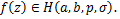 Then in view of (1.18), we have Then in view of (1.18), we have
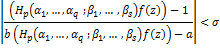
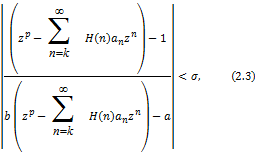
by using 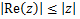 in (2.3), we get in (2.3), we get
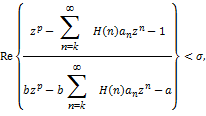
taking values of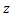 on the real axis and let on the real axis and let 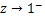 through real values then through real values then
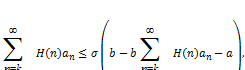
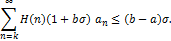
Conversely, let inequality (2.3) hold true, then
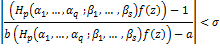
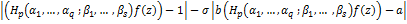
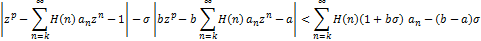
By maximum modulus principle, this implies that 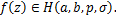
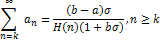
The result is sharp for the functions
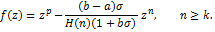
where 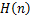 is defined by (1.9). is defined by (1.9).
Theorem 2.2. Let the function 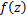 be defined by (1.4). Then be defined by (1.4). Then 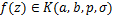 if and if and
only if
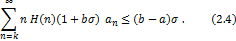
The result is sharp for the function
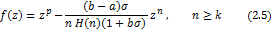
where 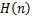 is defined by (1.9). is defined by (1.9).
Proof. On using (1.18) and (1.19), we easily arrive at the desired result (2.4) and (2.5).
3. Closure theorem
Let the function 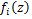 be defined for be defined for 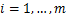 by by
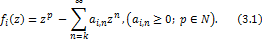
Theorem 3.1. Let the function 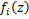 defined by (3.1) be in the class defined by (3.1) be in the class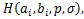 for each for each
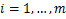 . Then the function . Then the function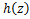 defined by defined by
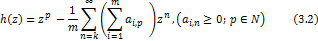
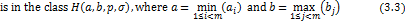
Proof.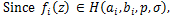 then by using (2.1) then by using (2.1)
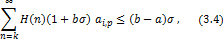
where 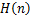 is given by (1.9). Therefore is given by (1.9). Therefore
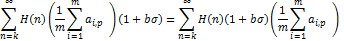
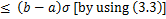
which shows that 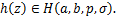
The theorem is completely proved.
Theorem 3.2. Let the function 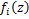 defined by (3.1) be in the class defined by (3.1) be in the class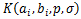 for each for each
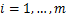 . Then the function . Then the function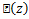 defined by defined by
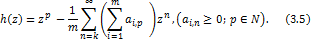
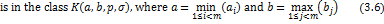
Proof. The proof follows exactly on the same lines as that of Theorem 3.1.
4. Distortion theorem for the classes 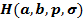 and and 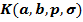
Theorem 4.1. Let the function 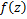 defined by (1.4) be in the class defined by (1.4) be in the class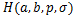 . Then . Then
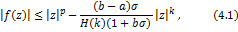
and
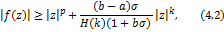
for 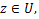 provided that provided that 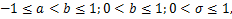 where where 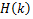 is defined by is defined by
(1.9).
Proof. by using(1.4), then we have
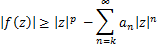
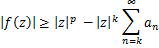
by using (2.1), we get
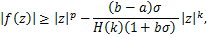
here 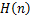 is defined by (1.9). is defined by (1.9).
We know that 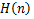 is non decreasing for is non decreasing for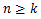 , then we have , then we have
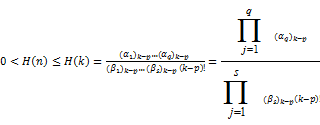 (4.3) (4.3)
Then,
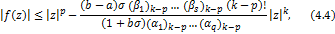
and
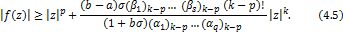
The theorem is completely proved.
Corollary 4.2. Under the hypothesis of theorem (4.1), 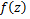 is included in a disc with it’s is included in a disc with it’s
centre at the origin and radius  given by given by
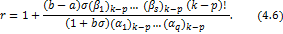
Theorem 4.3. Let the function 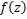 defined by (1.4) be in the class defined by (1.4) be in the class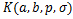 . Then . Then
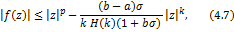
and
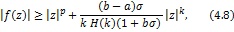
for 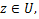 provided that provided that 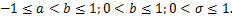
Where 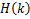 is defined by (1.9). is defined by (1.9).
Proof. On using (1.4) and (2.4), we easily arrive at the desired result (4.7) and (4.8).
Corollary 4.4. Under the hypothesis of theorem (4.2), 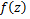 is included in a disc with it’s is included in a disc with it’s
centre at the origin and radius 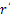 given by given by
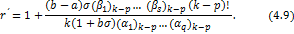
Theorem 4.5. Let the function 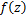 defined by (1.4) be in the class defined by (1.4) be in the class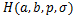 . Then . Then
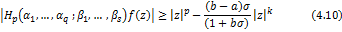
and
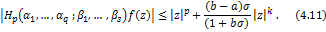
Proof. By using (1.8), we get
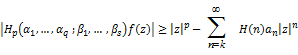 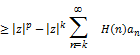 , (4.12) , (4.12)
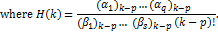
by using (2.1), (4.12) reduces to
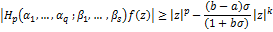
and
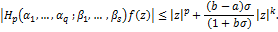
This completes the proof of theorem 4.5.
Theorem 4.6. Let the function 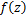 defined by (1.4) be in the class defined by (1.4) be in the class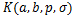 . Then . Then
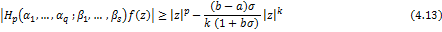
and
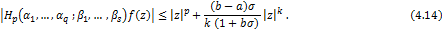
Proof. The proof follows exactly on the same lines as that of Theorem 5.1.
Corollary 4.7. Let the function 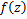 defined by (1.4) be in the class defined by (1.4) be in the class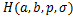 and let and let
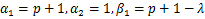 in (4.10) and (4.11) then it reduces to (4.15) and (4.16) in (4.10) and (4.11) then it reduces to (4.15) and (4.16)
respectively given by
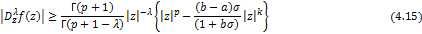
and
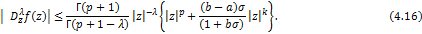
Corollary 4.8. Let the function 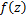 defined by (1.4) be in the class defined by (1.4) be in the class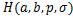 and let and let
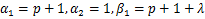 in (4.10) and (4.11) then it reduces to (4.17) and (4.18) in (4.10) and (4.11) then it reduces to (4.17) and (4.18)
respectively given by
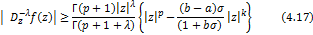
and
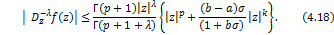
Corollary 4.9. Let the function 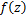 defined by (1.4) be in the class defined by (1.4) be in the class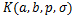 and let and let
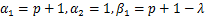 in (4.13) and (4.14) then it reduces to (4.19) and (4.20) in (4.13) and (4.14) then it reduces to (4.19) and (4.20)
respectively given by
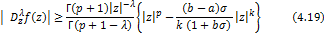
and
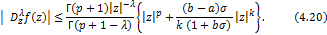
Corollary 4.10. Let the function 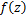 defined by (1.4) be in the class defined by (1.4) be in the class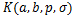 and let and let
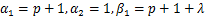 in (4.13) and (4.14) then it reduces to (4.21) and (4.22) in (4.13) and (4.14) then it reduces to (4.21) and (4.22)
respectively given by
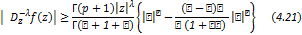
and
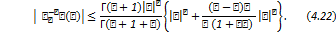
References
- E. Livingston (1966): On the radius of univalence of certain analytic functions, Proc. Amer. Math. Soc., 17, 352-357.
- C. Carlson and D.B. Shaffer (1984): Starlike and prestarlike hypergeometric functions, SIAM J. Math. Anal., 15, 737-745.
- H. M. Srivastava and S. Owa (1984): An application of fractional derivative, Math. Japonica, 29, 383-389.
- H. M Srivastava and M. K. Aouf (1992): Current topics in analytic function theory, World Scientific, Singapore.
- J. Dziok (1995): Classes of analytic functions involving some integral operator, Folia Sci. Univ. Tech. Resoviensis, 20, 21-39.
- J. Dziok and H. M. Srivastava (2003): Certain subclass f analytic functions associated with the generalized hypergeometric function, Integral Transform Spec. funct., 14, 7-18.
- R. K. Raina and T. S. Nahar (2002): On certain subclasses of
 valent functions defined in terms of certain fractional derivative operators, Glasnik Mathematicki, 37(57), 59-71. valent functions defined in terms of certain fractional derivative operators, Glasnik Mathematicki, 37(57), 59-71.
- R. J. Libera (1965): Some classes of regular univalent functions, Proc. Amer. Math. Soc., 16, 755-758.
- S. Owa (1978): On the distortion theorems, I Kyungpook Math. J., 18, 53-59.
- S. Ruscheweyh (1975): New criteria for univalent functions, Proc. Amer. Math. Soc., 49, 109-115.
- S. D. Bernadi (1969): Convex and starlike univalent functions, Trans. Amer. Math. Soc., 135, 429-446.
- Yu. E. Hohlov (1978): Operators and operations in the class of univalent function, Izv. Vyss. Ucsbn. Zaved. Matematika, 10, 83-89.
|


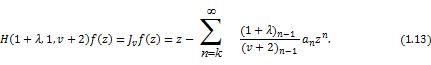
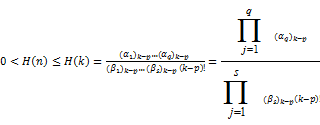 (4.3)
(4.3)